Cohérence et interférences

Pour comprendre le laser, nous avons besoin de connaître d’autres principes fondamentaux : la cohérence spatiale et la cohérence temporelle. La cohérence mesure la capacité des ondes à interférer entre elles. Deux ondes lumineuses sont dites mutuellement cohérentes si elles peuvent donner naissance à une figure d'interférence stable.

A. Cohérence spatiale

La cohérence spatiale possède en fait différentes propriétés. En effet, quand plusieurs ondes électromagnétiques respectent la loi de la cohérence spatiale, cela signifie que toutes les ondes sont orientées dans la même direction ; elles sont donc monodirectionnelles. De plus, elles ont une faible divergence et ont des phases identiques.
Comparons ceci avec la lumière blanche pour en donner un exemple simple.

La lumière blanche ne respecte pas la cohérence spatiale. En effet, puisqu’elle possède l’ensemble du spectre du domaine du visible, elle émet des photons différents dans toutes les directions. Elle n’est donc pas monodirectionnelle, n’a pas de phases identiques et ne possède donc pas de faible divergence.

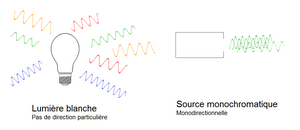
Ici, la source monochromatique est bien monodirectionnelle mais elle ne possède pas les mêmes fréquences ondulatoires.

B. Cohérence temporelle

La cohérence temporelle signifie qu’une onde ou groupe d’ondes possèdent tous la même fréquence et sont tous en phases, c’est-à-dire que les signaux des ondes sont synchronisés ; elles peuvent donc se superposer. Ainsi, dans un milieu composé uniquement d’un seul groupe de mêmes atomes, lorsque ceux-ci vont émettre des photons, ces derniers vont vibrer de la même manière ; ils vont respecter la cohérence temporelle.

À nouveau, nous pouvons dire que la lumière blanche ne respecte pas la cohérence temporelle. Puisqu’elle possède l’ensemble des ondes électromagnétiques du domaine du visible, toutes ces ondes ne vont donc pas vibrer de la même façon. Elles n’auront pas la même fréquence et donc ne vont pas respecter cette règle.

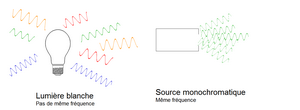
Ici, la source monochromatique possède les mêmes fréquences ondulatoires mais ces ondes ne sont pas monodirectionnelles.

À présent, combinons ces deux notions de cohérence.

C. Cohérence spatiale et temporelle

Un groupe d’ondes respectant simultanément la cohérence spatiale et temporelle va vibrer de la même manière, dans une seule direction en ayant une faible divergence. Le faisceau d’un laser exploite ces deux propriétés. Un laser est donc cohérent spatialement et temporellement car il possède un modèle capable de « fabriquer » des ondes qui respectent ces notions de cohérences, modèle que nous expliquerons dans la partie 3.

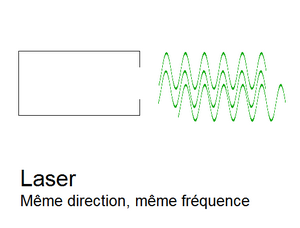
D. Interférences

Après avoir expliqué les notions de cohérences, nous allons passer aux interférences proprement dites.
Quand deux ondes identiques se rencontrent sous une certaine condition, il se produit ce qu’on appelle une interférence. Une interférence est un phénomène durant lequel deux ondes de même nature qui ont des périodes identiques vont se rencontrer et interagir entre elles, à condition qu’elles vibrent en phase à chaque instant. La figure résultante de l’interférence ne s’obtient pas seulement avec des ondes de type électromagnétique, mais peut se faire aussi avec des ondes sonores, lumineuses… Cependant, nous ne nous concentrerons exclusivement que sur les ondes électromagnétiques car elles sont la base du principe du laser.
En principe, il est pratiquement impossible d’observer des interférences avec des trains d’ondes de sources polychromatiques car non seulement il y a énormément de trains d’ondes différents émis (qui n’ont donc pas de même périodes), mais en plus ils sont émis à une telle vitesse (10^-11 secondes) que pour en faire interférer deux en même temps et qu’en plus, ils aient la même fréquence, et qu’ils vibrent tous en phase à chaque instant…
Une solution possible serait d’utiliser un faisceau laser. En effet, celui-ci possède des ondes de même fréquence, avec des trains d’ondes sensiblement plus grands et tous identiques. On pourra alors observer des figures d’interférence, étant donné que les trains sont beaucoup plus grands et peuvent interférer avec n’importe quel autre train, du moment qu’ils soient en phase.
Donc, quand deux trains d’ondes de même fréquence vont se rencontrer, trois cas seront possibles.

a) 1^er cas

Les trains d’ondes sont en phase. Il se passe alors un phénomène de superposition, phénomène où l’amplitude du signal est doublée. On parle alors d’interférences constructives. Il n’y a pas de différence de marche, c’est-à-dire, de décalage entre les deux ondes.

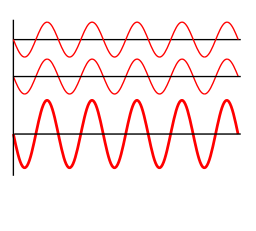
b) 2^ème cas

Les trains d’ondes ne sont pas parfaitement en phase. Il y a un léger retard de phase, une légère différence de marche. Il se produit alors une interférence légèrement destructrice.

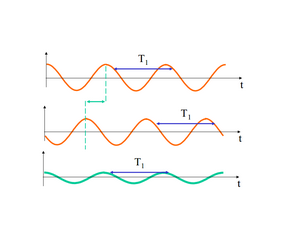
c) 3^ème cas

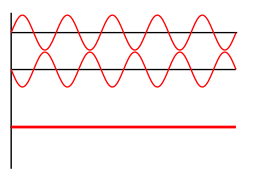
Les trains d’ondes ne sont plus du tout en phase. Ils sont en opposition de phase, ou plus exactement ils sont en déphasage. Il se produit alors un phénomène d’interférence destructive : il n’y a plus d’amplitude, donc de fréquence.

E. Les fentes de Young

Pour donner un exemple à ces trois types d’interférences, nous pouvons exploiter une partie de l’expérience des fentes de Young.
L'expérience consiste à montrer qu'un faisceau laser traversant deux fentes produit sur un écran une figure d'interférence, en envoyant deux grands trains d’ondes en phase mais sous un angle différent.
L’intérêt dans notre cas est d'avoir une image montrant comment se comportent deux trains d'ondes lorsqu'ils se rencontrent, nous pouvons ainsi l'analyser et la commenter.

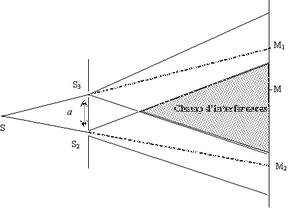
Sur cette zone grisée, plusieurs types d’interférences sont présents, et l’on obtient alors des figures d’interférences comme celle-ci :

Au centre, il y a des interférences constructives : on voit bien que la lumière y est plus intense, du fait du doublement de l’amplitude des signaux des trains d’ondes.
Plus on avance sur les côtés, plus les franges deviennent sombres. En fait, en ces endroits-là, il se produit des interférences légèrement destructives.
Là où il manque de la lumière, les zones noires, des interférences destructives sont présentes. Il n’y a plus d’amplitude, donc de lumière.

Ce patron d’interférence résulte d’une suite de phénomènes. Lorsque les ondes traversent les trous, elles vont alors subir la diffraction : la diffraction est le changement de direction de propagation d’une onde sans changement de sa longueur d’onde, au passage d’une petite ouverture ou d’un petit obstacle. Ainsi, quand deux trains d’ondes vont se rencontrer après l’obstacle, il se produira des interférences.

$Diffraction$

Vous pouvez aussi tester et obtenir des figures de diffraction en fonction de la longueur d'onde et de l'ouverture a en cliquant ici et pour expérimenter une diffraction en modifiant la taille de l'ouverture et de la fréquence, cliquez ici.
Je vous conseille aussi de visionner la vidéo qui suit. Elle parle entre autre, du saut quantique (à partir de 7:20) et de l'incroyable phénomène concernant les fentes de Young.